Benford's Law

Today we visit another of those counter-intuitive laws of mathematics, Benford's Law.

Wouldn't you think that the initial digit in in a large set of numbers would follow a random distribution? That's to say, wouldn't 1 as initial digit occur as frequently as 5 or 9?

Turns out, in practice, not to be so. (Although some sets of numbers - like lottery ticket numbers - don't follow the law).

The frequency of a digit n turns out to be f = LOG((n+1)/n), which looks like this: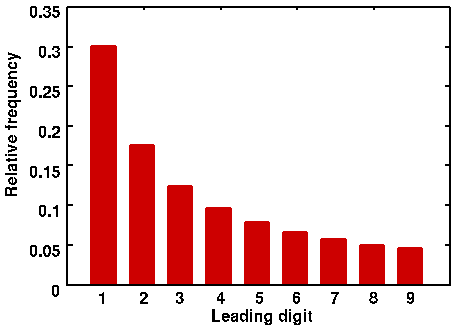



Details are available at the link above.